Метод линейной корреляции К. Пирсона
Коэффициент характеризует наличие только линейной связи между признаками, обозначаемыми, как правило, символами X и Y. Формула расчета коэффициента корреляции построена таким образом, что, если связь между признаками имеет линейный характер, коэффициент Пирсона точно устанавливает тесноту этой связи. Поэтому он называется также коэффициентом линейной корреляции Пирсона. Если же связь между переменными X и Y не линейна, то Пирсон предложил для оценки тесноты этой связи так называемое корреляционное отношение.
Величина коэффициента линейной корреляции Пирсона не может превышать +1 и быть меньше чем -1. Эти два числа +1 и -1 — являются границами для коэффициента корреляции. Когда при расчете получается величина большая +1 или меньшая -1 — следовательно произошла ошибка в вычислениях.
Знак коэффициента корреляции очень важен для интерпретации полученной связи. Подчеркнем еще раз, что если знак коэффициента линейной корреляции — плюс, то связь между коррелирующими признаками такова, что большей величине одного признака (переменной) соответствует большая величина другого признака (другой переменной). Иными словами, если один показатель (переменная) увеличивается, то соответственно увеличивается и другой показатель (переменная). Такая зависимость носит название прямо пропорциональной зависимости.
Если же получен знак минус, то большей величине одного признака соответствует меньшая величина другого. Иначе говоря, при наличии знака минус, увеличению одной переменной (признака, значения) соответствует уменьшение другой переменной. Такая зависимость носит название обратно пропорциональной зависимости.
Расчет коэффициента производился по формуле
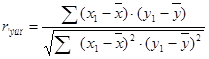, (2)
где x1 показатели уровня приязаний, а y1 показатели самоактуализации, 
и 
средние по выборке значения уровня притязаний и самоактуализации.
Описание выделенных групп
Все школьники, которых мы наблюдали, воспитываются в морально, экономически и психологически благополучных условиях. Все семьи полные, в воспитании принимают участие все члены семьи, в том числе и родственники более старшего поколения, у некоторых детей из выборки есть старшие братья и сестры. Наблюдения за детьми из двух выделенных гру ...
Понятие
профессионального отбора
Профессиональный отбор работников можно рассматривать как ориентацию и повышение квалификации работников - т.е. процесс, направленный на то, чтобы обеспечить их необходимой информацией, навыками, пониманием целей и задач предприятия. Ориентация облегчает поиски верного направления действий работника, способствует более быстрой адаптации ...
Орудийная деятельность
Человекообразные обезьяны используют орудия на воле и даже видоизменяют, подрабатывают эти орудия с целью наиболее эффективного применения их в деле. Именно они оперируют предметами интенсивнее всех млекопитающих, исключая, конечно, человека. Они отлавливают муравьев и термитов ветками, которые тщательно выбираются, очищаются от листьев ...
Разделы