Корреляционный анализ результатов исследования

Страница 1

Хотя на первый взгляд результаты первичного и контрольного исследования значительно отличаются друг от друга, мы не можем достоверно утверждать, что эксперимент удался. Для этого необходимо установить являются ли статистически достоверными между средними до и после эксперимента. Для установления статистической достоверности различий средних до и после эксперимента воспользуемся критерием Стъюдента. 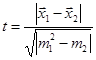, где – среднее значение переменной по выборке данных до эксперимента; - среднее значение переменной по выборке данных после эксперимента; m1 и m2 – интегрированные показатели отклонений частных значений из двух сравнимых выборок от соответствующих им средних величин. ; , где - выборочная дисперсия по первой переменной;- выборочная дисперсия во второй переменной; n1 – число частных значений переменной в первой выборке; n2 - частных значений переменной во второй выборке. Вычисляем средние значения переменной до и после эксперимента, воспользуемся критерием Стъюдента =27,2 = 33,5

Определяем выборочные дисперсии для двух сравнимых выборок значений. - первичное исследование. - контрольное исследование.

Подставим найденные значения дисперсий в формулу для подсчета m и t и вычислим показатель t: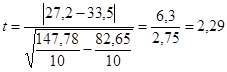

Сравним полученное значение с табличным для числа степеней свободы 10+10-2=18. Зададим вероятность допустимой ошибки, равной 0,05 и убедимся в том, что для данного числа степеней свободы и вероятностно допустимой ошибки значение t должно быть: . У нас этот показатель оказался равным . Следовательно, гипотеза, о том что выборочные средние равны в нашем случае 14, 778 и 8,265 статистически достоверно отличаются друг от друга и мы можем с достаточной убедительностью утверждать, что наша гипотеза подтверждается.

Для окончательного установления успешности формирующего эксперимента и окончательного утверждения нашей гипотезы воспользуемся статистикой, называемой , где Рk – частота результатов наблюдений до эксперимента; Vk – частота результатов наблюдений, сделанных после эксперимента; m – общее число групп, на которые разделились результаты наблюдений.

В нашем исследовании переменная Рк принимает следующие значения:

Р1=10% - процент учащихся имеющих высокий уровень социально-психологической адаптированности. Р2= 20% - процент учащихся имеющих нормальный уровень социально-психологической адаптированности. Р3= 70% - процент учащихся имеющих низкий уровень социально-психологической адаптированности.

Соответственно V1=10%; V2=40%; V3=50%.

Подставим все эти значения в формулу для x2 и определим его величину.

Воспользуемся теперь таблицей критических значений Х2-критерия /Р.С. Немов. Психология, стр 41/., где для заданного числа степеней свободы можно выяснить степень значимости образовавшихся различий до и после эксперимента в распределении оценок. Полученное нами табличное значение х2=25,71 больше соответствующего табличного значения m-1=2 степеней свободы, составляющего 13,82 при вероятности допустимой ошибки меньше, чем 0,1%. Следовательно:

Развитие личности
Салливан очень тщательно описал последовательность межличностных ситуаций, в которые вовлекается личность на пути от младенчества ко взрослости, и то, как эти ситуации влияют на формование личности. Большее внимание, чем другие теоретики личности, за исключением, может быть, Фрейда, Салливан уделил рассмотрению стадий развития личности. ...

Язык человекообразных обезьян
Люди издавна мечтали о возможности говорить с животными. Поэтому снова и снова они пытались научить пойманных детенышей человекообразных обезьян речи. Но успеха никто не добился. Обезьянам никогда не удавалось произнести ничего, кроме отдельных невнятных слов, и, уж конечно, их словарный запас не шел ни в какое сравнение со словарным за ...

Типы темперамнта и их психологическая характеристика
Темперамент – врожденные особенности индивида, проявляющиеся в интенсивности, темпе и ритме протекания психических процессов и состояний. Является биологическим фундаментом, на котором формируется личность. Темперамент человека отражается: · на скорости протекания психических процессов и их устойчивости (например, скорость воспроизвед ...